NumPy @ Operator (Matrix Multiplication in Python)

In NumPy, the @ operator means matrix multiplication.

For instance, let’s multiply two NumPy arrays that represent 2 x 2 matrices:

import numpy as np

A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])

product = A @ B

print(product)

Output:

[[19 22]
 [43 50]]

If you are familiar with matrix multiplication, I’m sure this answers your questions.

However, if you do not know what matrix multiplication means, or if you are interested in how the @ operator works under the hood, please stick around.

What Is Matrix Multiplication

A matrix is an array of numbers. It is a really popular data structure in data science and mathematics.

If you are unfamiliar with matrices, it is way too early to talk about matrix multiplication!

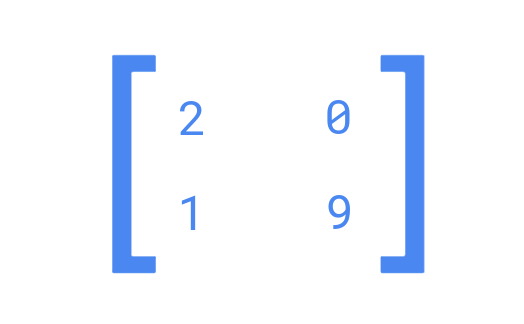
Multiplying a matrix by a single number (scalar) is straightforward. Simply multiply each element in the matrix by the multiplier.

For example, let’s multiply a matrix by 2:

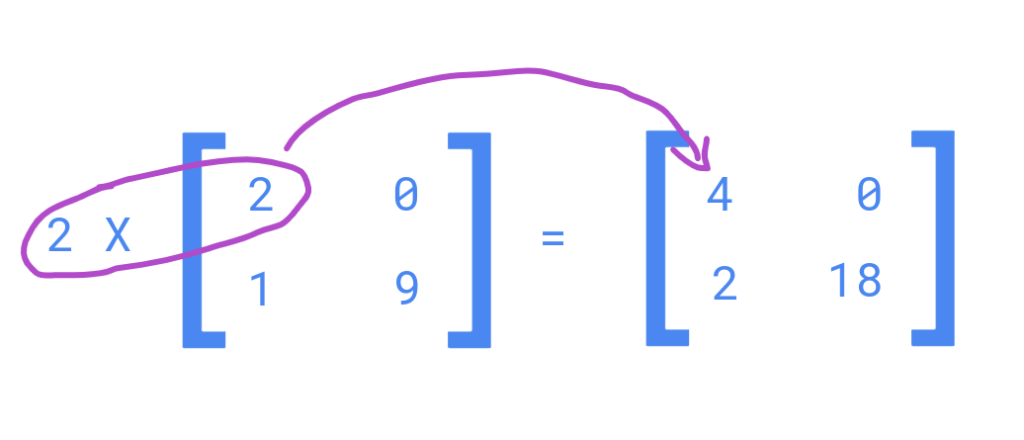
When you multiply a matrix by another matrix, things get a bit trickier.

To multiply two matrices, take the dot product between each row on the left-hand side matrix and the column on the right-hand side matrix.

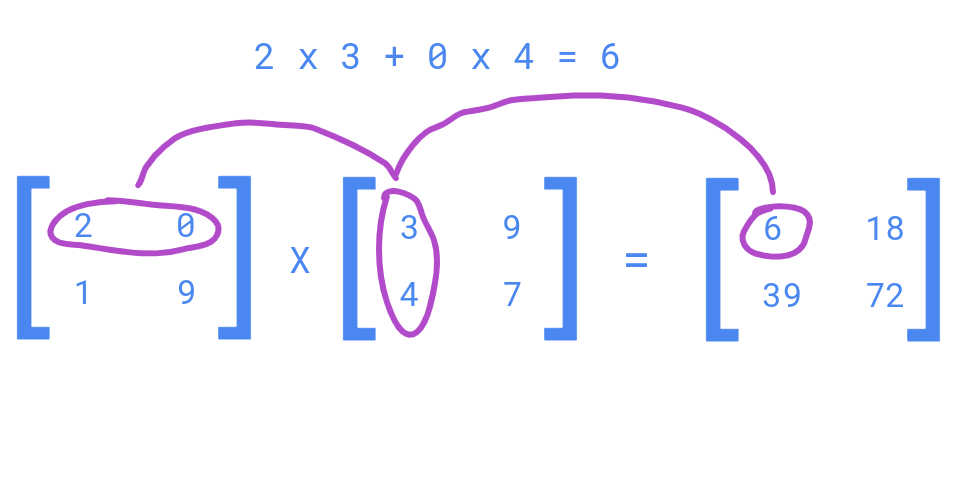
Here are all the calculations made to obtain the result matrix:

• 2 x 3 + 0 x 4 = 6
• 2 x 9 + 0 x 7 = 18
• 1 x 3 + 9 x 4 = 39
• 1 x 9 + 9 x 7 = 72

For a comprehensive explanation, feel free to check a more thorough guide on matrix multiplication here.

To keep it short, let’s move on to matrix multiplication in Python.

Matrix Multiplication in Python

To write a Python program that multiplies matrices, you need to implement a matrix multiplication algorithm.

Here is the pseudocode algorithm for matrix multiplication for matrices A and B of size N x M and M x P.

• Input matrices A and B
• Specify a result matrix C of the appropriate size
• For i from 1 to N:
  • For j from 1 to P:
    • Let sum = 0
    • For k from 1 to M:
      • Set sum ← sum + A_ik × B_kj
    • Set C_ij ← sum
• Return C

Let’s implement this logic in our Python program where a nested list represents a matrix.

In this example, we multiply a 3 x 3 matrix by a 3 x 4 matrix to get a 3 x 4 result matrix.

# 3 x 3 matrix
A = [
    [12,7,3],
    [4 ,5,6],
    [7 ,8,9]
]

# 3 x 4 matrix
B = [
    [5,8,1,2],
    [6,7,3,0],
    [4,5,9,1]
]

N = len(A)
M = len(A[0])
P = len(B[0])

# Pre-fill the result matrix with 0s.
# The size of the result is 3 x 4 (N x P).
result = []
for i in range(N):
    row = [0] * P
    result.append(row)
    
for i in range(N):
    for j in range(P):
        for k in range(M):
            result[i][j] += A[i][k] * B[k][j]

for r in result:
   print(r)

Output:

[114, 160, 60,  27]
[74,  97,  73,  14]
[119, 157, 112, 23]

As you might already know, matrix multiplication is quite a common operation performed on matrices.

Thus, it would be a waste of time to implement this logic in each project where you need matrix multiplication.

This is where the @ operator comes to the rescue.

The @ Operator in Python

As of Python 3.5, it has been possible to specify a matrix multiplication operator @ to a custom class.

This happens by overriding the special method called __matmul__.

The idea is that when you call @ for two custom objects, the __matmul__ method gets triggered to calculate the result of matrix multiplication.

For instance, let’s create a custom class Matrix, and override the matrix multiplication method to it:

class Matrix(list):
    # Matrix multiplication A @ B
    def __matmul__(self, B):
        self = A
        
        N = len(A)
        M = len(A[0])
        P = len(B[0])
        
        result = []
        for i in range(N):
            row = [0] * P
            result.append(row)
            
        for i in range(N):
            for j in range(P):
                for k in range(M):
                    result[i][j] += A[i][k] * B[k][j]
        return result
        
# Example
A = Matrix([[2, 0],[1, 9]])
B = Matrix([[3, 9],[4, 7]])

print(A @ B)

Output:

[[6, 18], [39, 72]]

As you can see, now it is possible to call @ between two matrix objects to multiply them.

And by the way, you could also directly call the __matmul__ method instead of using the @ shorthand.

# Example
A = Matrix([[2, 0],[1, 9]])
B = Matrix([[3, 9],[4, 7]])

print(A.__matmul__(B))

Output:

[[6, 18], [39, 72]]

Awesome. Now you understand how matrix multiplication works, and how to override the @ operator in your custom class.

Finally, let’s take a look at multiplying matrices with NumPy using the @ operator.

Matrix Multiplication with NumPy: A @ B

In data science, NumPy arrays are commonly used to represent matrices.

Because matrix multiplication is such a common operation to do, a NumPy array supports it by default.

This happens via the @ operator.

In other words, somewhere in the implementation of the NumPy array, there is a method called __matmul__ that implements matrix multiplication.

For example, let’s matrix-multiply two NumPy arrays:

import numpy as np

A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])

product = A @ B

print(product)

Output:

[[19 22]
 [43 50]]

This concludes our example in matrix multiplication and @ operator in Python and NumPy.

Conclusion

Today you learned what is the @ operator in NumPy and Python.

To recap, as of Python 3.5, it has been possible to multiply matrices using the @ operator.

For instance, a NumPy array supports matrix multiplication with the @ operator.

To override/implement the behavior of the @ operator for a custom class, implement the __matmul__ method to the class. The __matmul__ method is called under the hood when calling @ between two objects.

Thanks for reading. Happy coding!

Further Reading

How to Transpose a NumPy Matrix